Self-Balancing Robot
Capstone: Reaction-Wheel Inverted Pendulum
Jan. 2024 - Present
This prototype is a part of a team Capstone project, in which we are surveying different controls strategies for robots with unstable dynamics. We are mainly comparing the performance of traditional controls methods including using PID controllers, using a Linear-Quadratic Regulator, and using a Model-Predictive Controller, with the performance of neural-network-based controllers, mainly using Reinforcement Learning.
What makes this problem interesting?
One of the main challenges of this project is characterizing the dynamics of our robot. The video depicts a prototype, but our main robot has a motor in each of the three axes. This brings about highly complex dynamics equations due to phenomona such as gyroscopic procession, and the conservation of angular momentum.
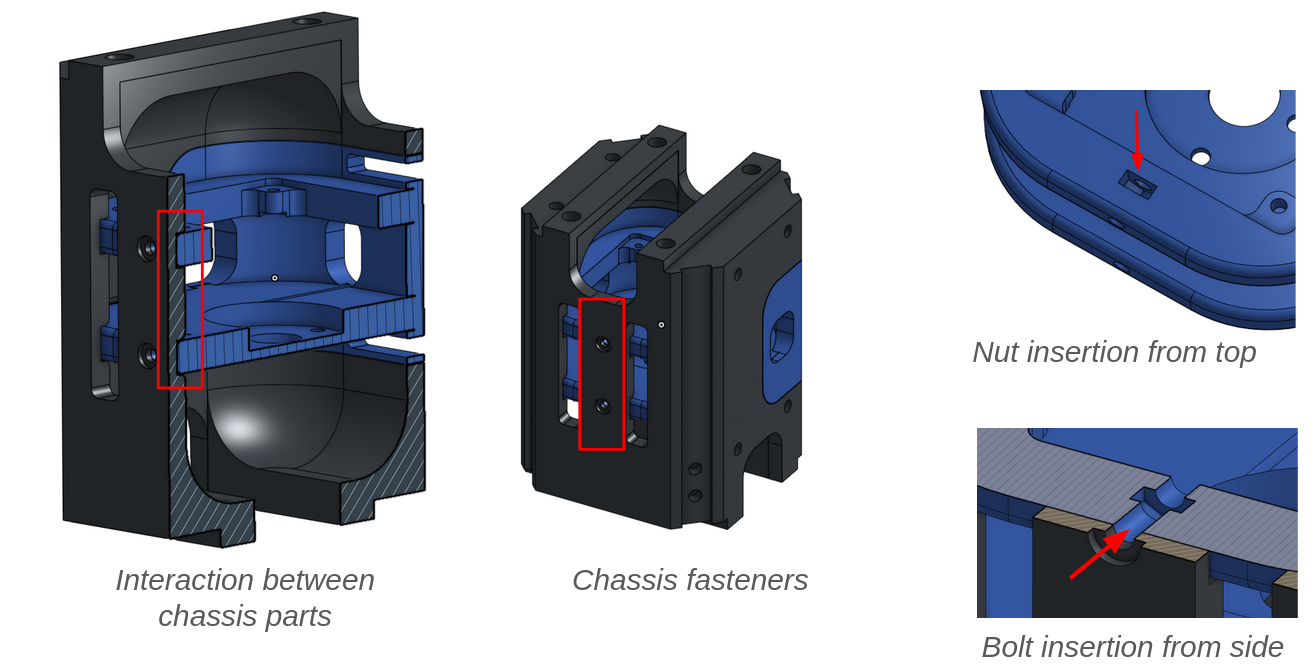
I personally worked on the CAD design of the robot. I created a CAD design that could be 3D printed that had the following benefits from the original:
- reduced number of parts, easing assembly
- reduced number of fasteners required
- impact loads taken by 3D printed parts, allowing for smaller, lighter fasteners to be used, reducing total mass.
LQR and MPC controller development
The gains for the LQR controller are calculated using an optimization algorithm, which takes a sort of cost function as its input. Therefore, the controller is only good as your cost function is, as for any given cost function, the LQR optimization will create an optimal controller to minimize the given function.
In our case, our cost function mostly uses the angles of the robot, measured from upright, so that the optimized controller tries to minimize the angle of the robot, keeping it balanced. Additionally, the physics of electric motors create some challenges: All electric motors have a maximum speed, at which torque cannot be further applied in the direction of rotation. Therefore, we need to penalize high motor speeds to make sure the controller never gets itself to a point where it can no longer apply a torque, otherwise it may be unable to self-right. This is a tricky problem that goes beyond classical control theory (at least, at the level we are taught in undergraduate engineering).